In This Article
Note: See the end of this post to see how you can get/use my expense tracking spreadsheet (free).
Many people are interested in how much around-the-world (RTW) or other long-term travel costs, especially as a budget traveler or backpacker. As I explained in my Central America cost breakdown, before I began my multi-year Latin America journey, I created a spreadsheet to track my expenses. Believe it or not, I managed to maintain it and now have complete expense data to share with all who might be interested. Now that I have finally left Brazil I can provide the full details for South America.
How I Travel and Other Observations
Any breakdown of this nature deserves some background information, and the value of my particular expenditures tracking will naturally depend on how similar your travel style is to mine. Perhaps the best description of my travel style is comfortable cheap. Whenever possible I try to save costs but I am not on such a tight budget that I will put up with extremely unpleasant or unsafe circumstances just to save a little money. In my previous post I listed many more details, based on the categories I tracked, of how I travel to help you understand my numbers better so read that if you are interested. To recap I will just list the basic ideas here:
- For lodging, I prefer a private room if it is reasonably priced, but otherwise I am fine with staying in dorms. I stayed one month in an apartment in Medellín, 4+ months in an apartment in Buenos Aires and about three months in an apartment in Salvador da Bahia, each time renting a room rather than the entire apartment.
- I am not a foodie and generally either prepare food myself or eat at cheaper local establishments with the occasional nicer meal.
- I am not much of a drinker so I save a lot of money in that category.
- As a slow traveler, I usually take buses and break up long distances with visits to places closer along the way. I did take one round-trip flight in Bolivia (part of an Amazon tour), a one-way flight in Chile from Puerto Montt to Punta Arenas, and two one-way and one round-trip flights in Brazil. I usually prefer local buses or walking to taxis.
- I note my major tourism expenses where appropriate below. Clearly, my biggest tourism expenditure was my trip to Antarctica, which was expensive but worth every penny.
- I didn’t take any classes in South America.
- My apartments in Medellín and Brazil had a washing machine but otherwise I used laundry services.
- I used pre-paid phone service in Argentina and Brazil. I bought three mobile phones in two years. The first I bought in Lima but it was stolen by the notorious pickpockets in Buenos Aires. The second I bought used to replace that one. The third I bought in Ciudad del Este because it turned out the Argentina phone was dual-band and wouldn’t work in Brazil (yes, I asked about the bands when I bought it but it was used and they lied to me). A note: cheap phones are plentiful in Central America, often coming with enough free calling credit that the phones are basically free. This is NOT the case in South America so bring an unlocked phone with you.
- All dollar figures are based on my actual exchange rates at the time (averaged) and all euro numbers are those same dollar numbers converted at today’s Internet exchange rate for dollar-euro.
- I haven’t included pre- or post-travel costs, such as my flight to leave Brazil (ending my Latin America journey), the electronics I bought before leaving, insurance, original clothing, etc. Basically I am only including what I spent on the road.
Costs by Country
Overview
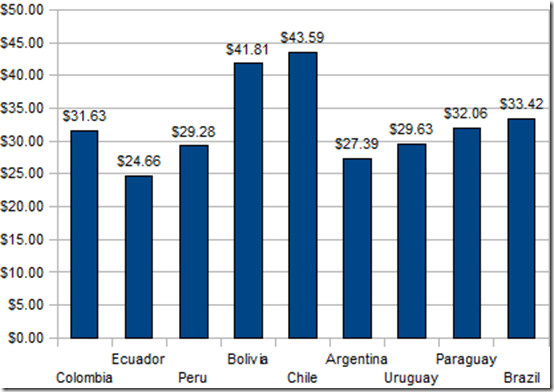
Overall, in South America, I spent 669 days and US$20,717 for an average of US$31 per day. These numbers don’t include my trip to Antarctica which I detail later. See the notes for each country to better understand the numbers.
| Country | Days | Total Cost | Daily Cost | ||
|---|---|---|---|---|---|
| Colombia | 98 | $3,099.79 | €2,324.84 | $31.63 | €23.72 |
| Ecuador | 45 | $1,109.58 | € 832.59 | $24.67 | €18.50 |
| Perú | 57 | $1,668.94 | €1,251.71 | $29.28 | €21.96 |
| Bolivia | 35 | $1,463.34 | € 970.87 | $38.07 | €28.55 |
| Chile | 23 | $1,002.65 | € 751.99 | $43.59 | €32.70 |
| Argentina | 214 | $5,862.13 | €4,396.60 | $26.17 | €19.63 |
| Uruguay | 16 | $ 474.12 | € 355.59 | $26.17 | €19.63 |
| Paraguay | 9 | $ 288.56 | € 216.42 | $32.06 | €24.05 |
| Brazil | 172 | $5,747.63 | €4,310.73 | $33.42 | €25.06 |
| Total | 669 | $20,716.76 | €15,537.57 | $30.97 | €23.23 |
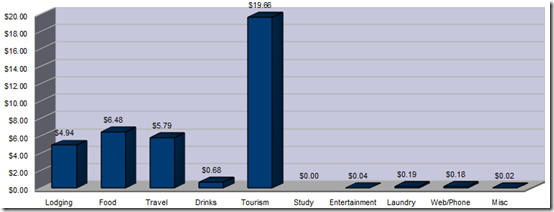
Colombia
My costs in Colombia were slightly higher than might otherwise be expected because I chose to rent a somewhat expensive room in an apartment in Medellin for a month. Also, I had my camera stolen and had to buy a new one so that added to my overall expenses.
Ecuador
Ecuador ended up being the least expensive country. I had originally hoped to visit the Galapagos islands which certainly would have blown up the budget, but in the end I decided against it as I didn’t want to go in the off-season. My lodging numbers could have been a bit lower if I had stayed in dormitories but as you can see, staying in private rooms was hardly an unreasonable expense. Plus, in some places there really aren’t typical hostel with dorm options. That fact also meant I rarely cooked because there was usually no kitchen but as you can see my food budget wasn’t too bad anyway.
Peru
I did more tourist activities in Peru such as sandboarding, the poor man’s Galapagos, Colca Canyon, the Cuzco tourist ticket and, of course, Machu Picchu. None of these expenses were in any way unreasonable. Travel was more than double my Ecuador numbers, partly because buses cost about double and partly because it is a larger country and I was moving around a fair amount. Finally, I bought both a new pair of hiking boots and a simple smart phone in Peru, which drove up the daily average more than five dollars.
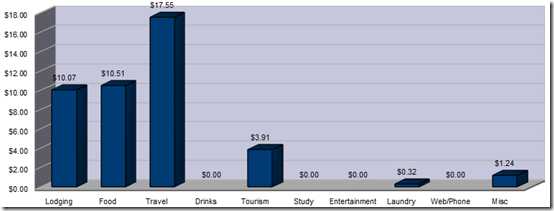
Bolivia
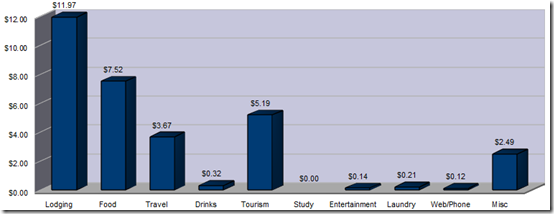
Bolivia is generally considered a cheap country, and it certainly can be, but for me you’ll notice it wasn’t so much. That is because I had to pay US$135 for a tourist visa and I did three touristy things that cost some money: bicycling the death road, climbing Huayna Potosi and doing an Amazon tour (worth every penny though each!). Also, I didn’t spend as much time in Bolivia as I would have liked because I knew I had to get down to Ushuaia for my trip to Antarctica before the season ended in March. Note that I purchased a sleeping bag and some extra cold-weather clothes in La Paz which I lumped in the tourism category when I probably should have put them in the miscellaneous category instead.
Chile
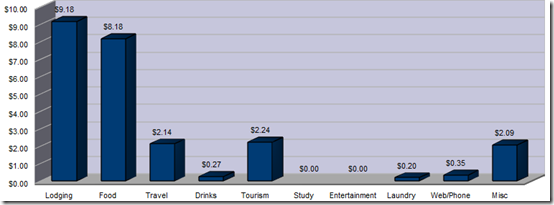
As you can see, I spent far less time in Chile than in other countries (still rushing to get to Antarctica) and it is a very long country, thus travel costs were my biggest expense. That included one flight from Puerto Montt to Punta Arenas. It cost about 50% more than the bus ride, but saved me 24+ hours of travel time and the need to cross the Chile/Argentina border twice. I switched from private rooms to dormitories in Chile otherwise my lodging numbers would have been much higher. The tourism costs were mostly attributed to my week hiking in Torres del Paine.
Antarctica
There is no point breaking down the expenses for my trip to Antarctica as it was an all-inclusive cruise. I paid $3490 for the cruise and added a $110 tip for a total of $3600. You could (and should) argue that I paid more because I had to stay extra days in Ushuaia while I searched for and then waited for my cruise. Those costs are, instead, bundled in my Argentina numbers. Likewise, you should factor in transportation expenses to get to Ushuaia but, in my case, I would have visited that city regardless.
Argentina
In Argentina my lodging costs included almost five months renting a room in an apartment in Buenos Aires. Food definitely would have been a bigger expense if I wasn’t cooking for myself so often. Staying for so long, I did buy a cheap used phone (after the one I bought in Lima was pickpocketed on the subway) and I used pre-paid service. Mostly I just used the phone for sending text messages so my costs weren’t significant.
One big point I should make is that Argentina is experiencing very high levels of inflation. For example, when I arrived in Buenos Aires, a pizza at Ugi’s, a chain (not that great, but generally cheap) was AR$14 (and I was told it had just recently increased from AR$12). When I left 5 months later it was AR$21. The government lies about the real level of inflation but it is generally believed to be at least 30% per annum. In theory, if the exchange rate adjusted in step with inflation foreign travelers wouldn’t need to worry so much and my numbers would probably stay more or less accurate but in my experience the exchange rate did not in fact move in proportion to inflation. It was about US$1 = AR$4 when I arrived and when I left it was US$1=AR$4.2 (5% change).
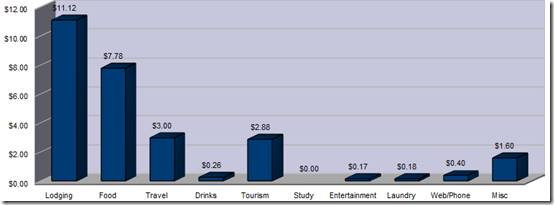
Uruguay
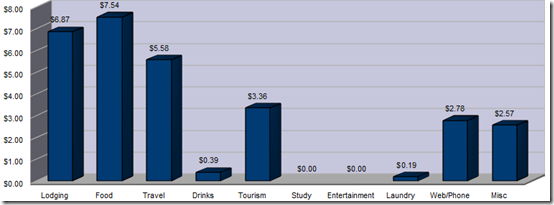
I traveled fast in Uruguay, mostly because the interesting things to see aren’t that numerous and cover a fairly small geographical area (for South America). Also, it was low season and still a bit chilly so the main attractions, the beaches, weren’t really worth extended stays. I mostly ate out and it is reflected in my food costs. My travel costs would have been higher but I was fortunate to make friends with an Argentine guy who was on vacation with his car and we traveled together a bit with him refusing to allow me to pay for any gas.
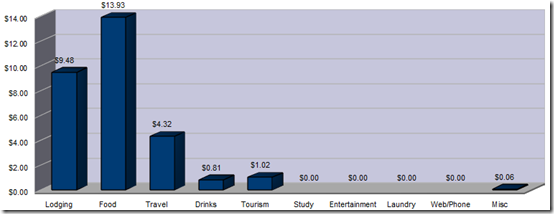
Paraguay
My Paraguay visit was very short, and confined to Asunción. There were some things I had originally wanted to do but in the end I lost my energy and was anxious to get back to Brazil, especially so I could see some things before the high season began. My average costs were driven significantly higher mostly due to the fact that I had to pay US$100 for the visa. Also, my lodging was higher than it needed to be, but I had a very nice private room which I definitely thought was worth the money. It wasn’t permitted to use the kitchen so I ate out every day for lunch and dinner which drove my food costs up.
Brazil
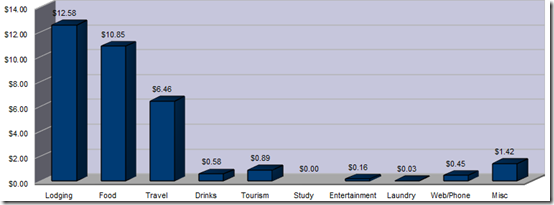
One thing you will invariably hear if you talk with other backpackers is that Brazil is expensive. Not expensive like Australia but definitely expensive for South America. My numbers don’t really reflect that, mostly because I spent almost six months in the country and rented a room in an apartment for more than half of that time. Overall I do think things are more expensive in Brazil, especially transportation and dining out (though there are quite a few cheap food options available as well). Brazil is a huge country and, interestingly, the prices vary a lot from one part of the country to another. Generally speaking, the further south you go the more expensive things get. Most of the tourism money I spent was due to the tourist visa I had to purchase (about US$150 for the first time and about US$35 for the renewal).
How I Track My Expenses: Get the Spreadsheet Yourself
As with my Central America breakdown, I tracked all my South America expenses using my custom-built travel expenses tracking spreadsheet. If you’d like a copy for yourself, just click through for the public Google Doc, or if you prefer an Open Office version, just contact me directly and I will be happy to email you a copy. The spreadsheet will automatically convert to US dollars and Euros; it can handle a variable number of days, up to 366 (accounting for a leap year), though there is a smaller one-month worksheet as well for shorter trips; and it will automatically graph your expenses. If you do use it and find any errors please let me know.
Finally…
Spending Breakdowns Around the Web
In my Central America cost breakdown I listed quite a few similar budget breakdowns from other bloggers that I have come across which you might want to check out. Alternatively, Jodi at Legal Nomads offers a resources page with a good collection broken down by RTW and part of the world.
Click to See or Add Your Own »

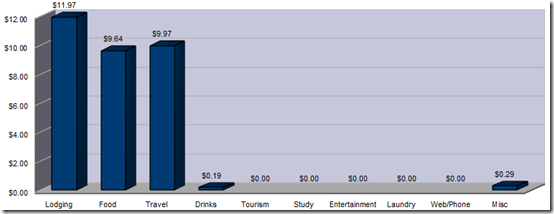
I was shocked when I saw your Bolivia numbers, but you are right that if you don't spend much time there, you don't spread out the cost of the tourist visa and the big tour expenses.
Yes, without the visa and other tourism costs the daily average would have been less than $20. I hope you enjoy your stay there!
Really a sound analysis of travel expanses and pretty hopefully here shared analysis of travel expanses will be handy for counting my whole year travel cost. Thanks
Paraguay sure looks like a tempting option for budget travelers. I’m a little surprised how much lower the cost is though compared to other countries in the area.
Hey, thanks a lot for the detailed expenditure; just what I was looking for in order to properly budget for our SA trip. Sounds like your lifestyle matches ours so great reference for us. Really grateful for you having shared this info with us!
Best regards,
Joe
Glad you found it useful. Enjoy your trip!
Thank you so much for posting this! VERY HELPFUL!!!
Are you not from the U.S.? The majority of countries in Latin America do not require a visa for U.S. citizens.
Well, what I'm really asking is…why were you required to pay so much to enter most countries in South America? I thought with U.S. passports we didn't need visas. What was the procedure at each border crossing? Thanks!
Yes, I am from the U.S. and I'm not sure what you mean by "most" countries. I had to pay for a visa to enter Bolivia, Paraguay and Brazil. I believe a visa is required for Suriname as well but can't recall about the Guyanas (didn't visit any of those). As for amount, my understanding is that price is usually reciprocal, that is to say they charge us what we charge them to enter the U.S. Procedures vary so you should do your research before traveling. Bolivia can be done at the border (though it is better to do before crossing if you are able). Brazil must be done in a consulate before entering and I believe the same is true for Paraguay. Some people get confused about visa issues when flying in to Chile or Argentina because there is a fee to be paid (or, at least, there used to be, not sure if there still is). This fee is NOT for a visa however.
did you pay to get into argentina …..i think it is a reciprocity fee. I'm trying to plan a trip to SA and would appreciate any info. you could give on avoiding reciprocity fees. I will stay to countries that don't charge – whenever possible. But, if I have to , I will go to others.( preferably by sneaking in). I know it is a bad and dangerous choice but my budget dictates my behavior. thanks for any help you can give –
Argentina only charges at the airport if you fly in. It isn't a visa fee. So, want to avoid paying, fly into a different country and enter Argentina by land. Have a good trip.
Unfortunately now you need an Argentine reciprocity fee (if you're from US) even to cross by land, and you have to buy it online ahead of time. Chile however you only have to pay at the airport.
Thanks for the update – I wasn't aware of that change.
Thanks for breaking it down so well. Just deciding what countries I'll be visiting in South America and this is really helpful.
nicely explained in bar chart…
good work…. 🙂
I believe a visa is required for Suriname as well but can’t recall about the Guyanas (didn’t visit any of those). As for amount, my understanding is that price is usually reciprocal, that is to say they charge us what we charge them to enter the U.S. Procedures vary so you should do your research before traveling.
I would like to know how did you rent your room
from where did you get the inform ? to rent it.
I don't remember the specific websites I used, but in Medellin I think it was Craigslist, which generally had overpriced places geared towards gringos. In Buenos Aires there are several decent websites for finding a room to rent. I think one was compartodepto.com. In Brazil I found my room to rent by luck, running into a girl who had rented the room previously while I was traveling.
Hey.
Could you possibly quickly go over what the apartment costs were in the different countries you rented (either full apartment or just private room in the apartment)
Im currently planning a trip from RIO up through 8 countries to Colombia and am weighing my options. I plan on volunteering at some hostels to cut costs, but would be interested to see the cost differences between a hostel (anywhere from $8 to $20 a night dorm room) and a private room in an apartment.
Thanks in advance.
Sorry, I really don't remember those details, but I always rented a room in a shared apartment and I am sure the price was competitive or less than a hostel alternative. Have a great trip.
Great blog! Thanks so much for the detailed work. By the way you mentioned you had a great room in Paraguay…
I wonder if you chose a hotel, hostel or some other place to stay?
Ali
I am not sure I would say I had a great room. I did have a private room rather than a dorm, and it was good, but nothing special, though I liked the family atmosphere and met some nice fellow travelers there. Consulting my notes, I think I stayed at Pensión da Silva (I have a few places listed in my notes so I am not 100% sure but I think that was the place).
Hi mate,
Great read – very well written and laid out, just in question – Where did you find the accommodation you stayed in? If you could give any pointers as to the places you stayed that would be brilliant.
What were the main places you visited whilst in South America, i noticed as well you mentioned Paraguay and places you didnt get to visit, and was wondering what those places were if i were to explore around.
Thanks for the detail and great read mate.
James
It has been quite a while since that trip so my memory is fuzzy. For accommodations I used multiple sources – hostel booking sites, guidebook recommendations, suggestions from fellow travelers and sometimes just from walking around and looking. As for the main places, that is a big question that I don’t know how to begin answering. I did a few less-known places but mostly I visited the well-known places discussed online and in guidebooks. I have individual country posts for most of South America so you can see exactly where by reading those. I think I discuss the places I stayed as well in those posts.
Hey, thanks for the great breakdown. Im starting my SA research.
Do u think would have to double the daily budget to allow for more adventure/touristy activities and the more regular alcoholic drink?
Cheers for the help 😀
I don’t have a good answer. As I recall, beers are pretty cheap all over South America, often only about US$1-2 for a litre bottle so that shouldn’t hurt your wallet too much, but I have no idea about mixed drinks. I didn’t really avoid touristy or adventure activities so I am not sure what exactly you have in mind in that sense. Regardless, I hope you have a great trip.
Very interesting trip and I’m looking to do the same if I can retire soon. My one question would be how did you do the money? I picture my bank at home depositing ex-amount of money each month so I could draw on it from the ATM’s through out the different countries and never having “to much” money in the account a any one time. did you ever have any problems getting money? I’m assuming you were mostly on a cash basis rather than a credit card.
That’s more or less what I did. I have two bank accounts and I occasionally used online banking to transfer funds from the first account to the second account I used for ATM withdrawals. Since I am from the USA, there are a couple of account options (Schwab, Fidelity) that offer ATM fee reimbursement anywhere in the world, so that is naturally my go-to ATM account. I think similar types of fee-free accounts exist in some other countries (Canada, maybe UK, not sure which exactly) so do some research before you leave. Have a great trip!
Excellent post! we try to keep our budget as low as possible traveling. Hi Marek, we traveled through Latin America for 13 months. I thought you might find my overview of South America interesting.
We spent $3881 in 275 days so an average budget of $14.11 each per day.
We traveled all South American countries on a tight budget, it is very possible. The cost of travel in each country is not only dependent on price. Some examples; Chile is an expensive, but safe country that is very camping and hitchhike friendly and it is possible to hike independent. In contrast Bolivia is a cheap country, but crime can be a problem and activities are expensive. Consequently we spent more per day in Bolivia than Chile.
Safe Travels
http://stingynomads.com/south-america-travel-budget/
What a great post, extremly helpful, thank you for taking the time to do this and share it with us.
Thanks for the great breakdown! Your numbers are from about 6 years ago and I was wondering if you’ve been back to any of these countries since and if the numbers have changed drastically? My husband and I are doing a similar, albeit faster, 4 month trip through Equador to Brazil (skipping Paraguay unfortunately). Any info you can share would be great! Thanks,
Heather
Unfortunately, I have not been back since then. I imagine prices have changed quite a bit. It would be great if you would post some updated prices and information here after you finish your trip. I hope you have a great experience.